Lecture #1.

We had our first lecture today and the very first activity got everyone thinking and working on numbers already. Throughout the first lecture, the many activities allowed me to approach math in a different manner. Instead of looking at them as a "problem" to "solve", I realised that what was waiting to be discovered were number patterns that would in return help to decode and unravel the solution. It was especially exciting trying to figure the pattern to the cards (lesson and activity 4). My partner and I worked backwards and started with card #9 and #8. We eventually got on until #5 but somehow our method couldn't work with #4 onwards... I still wonder why and would definitely want to figure that out still!

We also learnt the different uses of numbers in this session and how we as educators should present them to children in the right manner and at the suitable time for them to grasp and understand.

• Ordinal numbers - used to indicate position with respect to space and time. 
• Number patterning - a child's possible first number pattern is introduced in rote counting where there is an addition of 1 to the next number.
• Rational counting (cardinal numbers) - there are two forms, namely discreet and continuous to count quantities. In rational counting, units of measure are eventually introduced (around Primary 2) but not in the initial stage of counting.

I learnt through this lecture as well that the ten frame is a useful tool for a teacher to gain insight on where a child stands in terms of having "number facts". E.g: The ability to "see" from the frame that 10 and 2 make 12, 5 and 7 make 12, and even other patterns, etc.

These are a list of things that teachers can take note of in terms of a child's mathematical level of understanding and capability from a child's work and interaction on a ten frame.

• Counting all - child is be able to begin counting from 1. 
• Counting on - for example in the sum 3 + 4, child begins counting on from 3 (or even 4) and does not fall back to begin counting from 1. 
• Counting on with commutative property of addition
• Skip counting 
• Conservation of numbers
• Advanced emerging ability in place value

What stayed with me the most for this lecture is seen in the picture that follows.

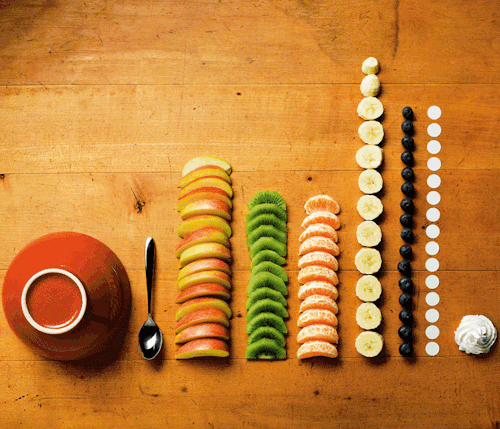
In the English language, we have countable and uncountable nouns. In Mathematics, we also have countable and uncountable things. This picture is an example of a group of things that cannot be counted. Yes, we can still count how many items there are in total. However for a young child beginning to count, it would be a confusing task to accomplish. For children, counting should first be introduced with identical things (e.g. buttons of the same kind, same unit, same set). They can then be moved on to counting in identical sets before eventually moving on to the nonidentical things. This picture of things is therefore uncountable for young children.